|
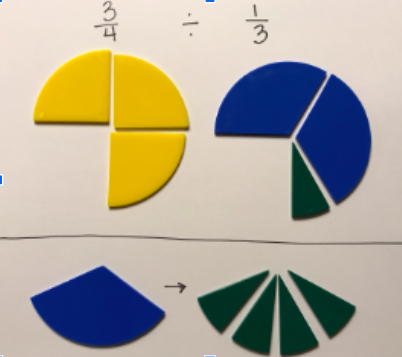
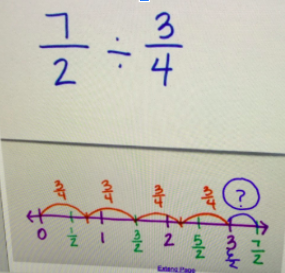
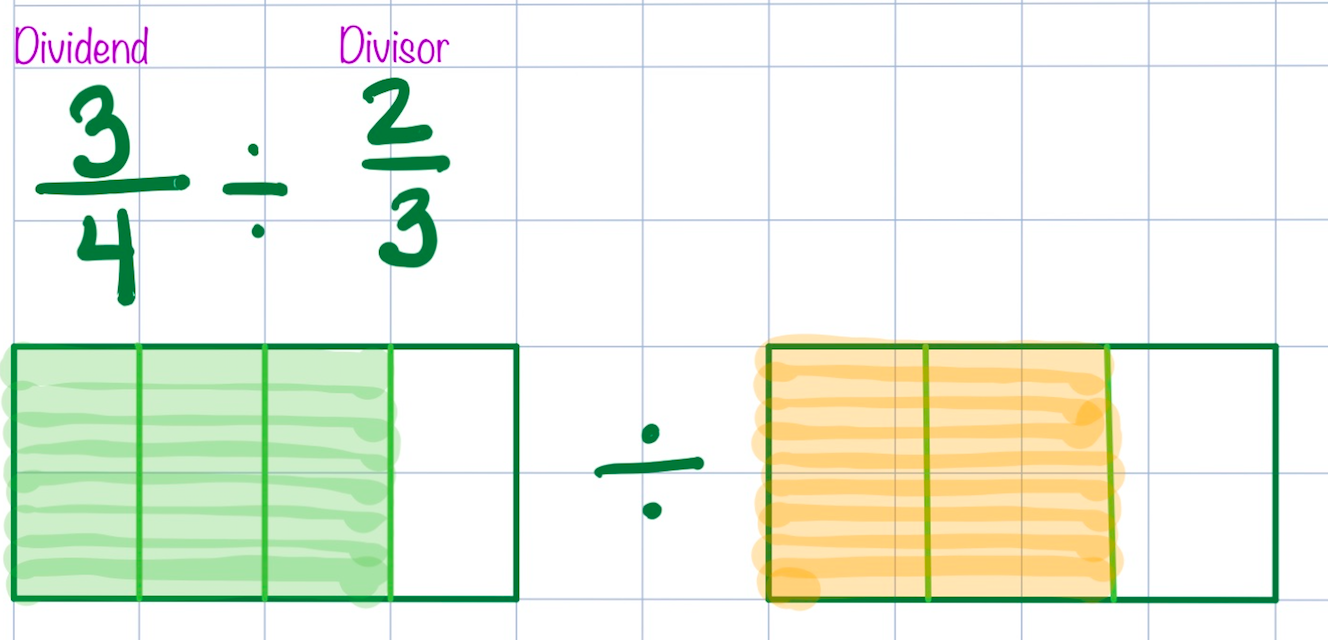
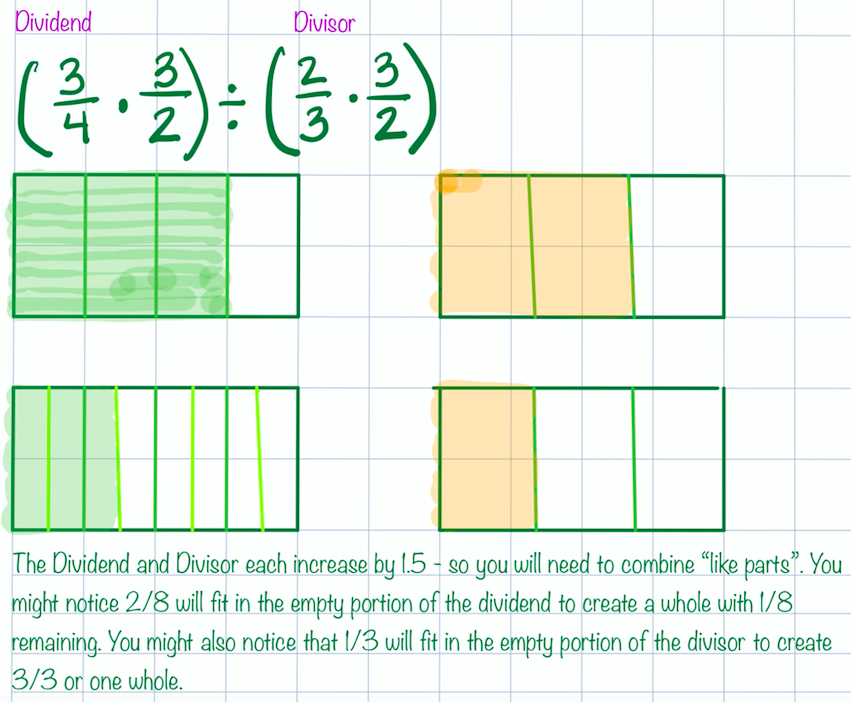
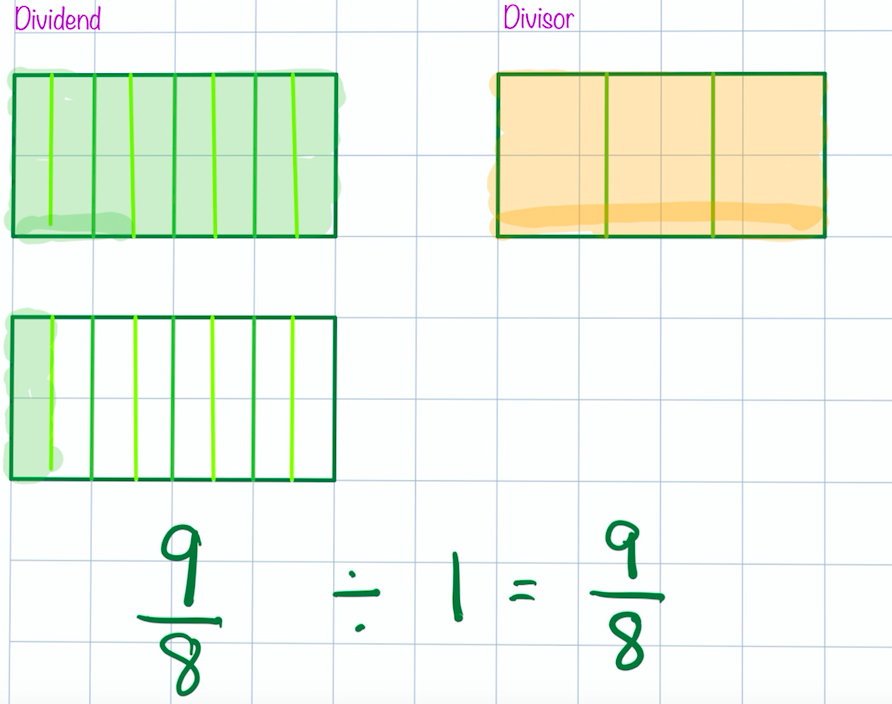
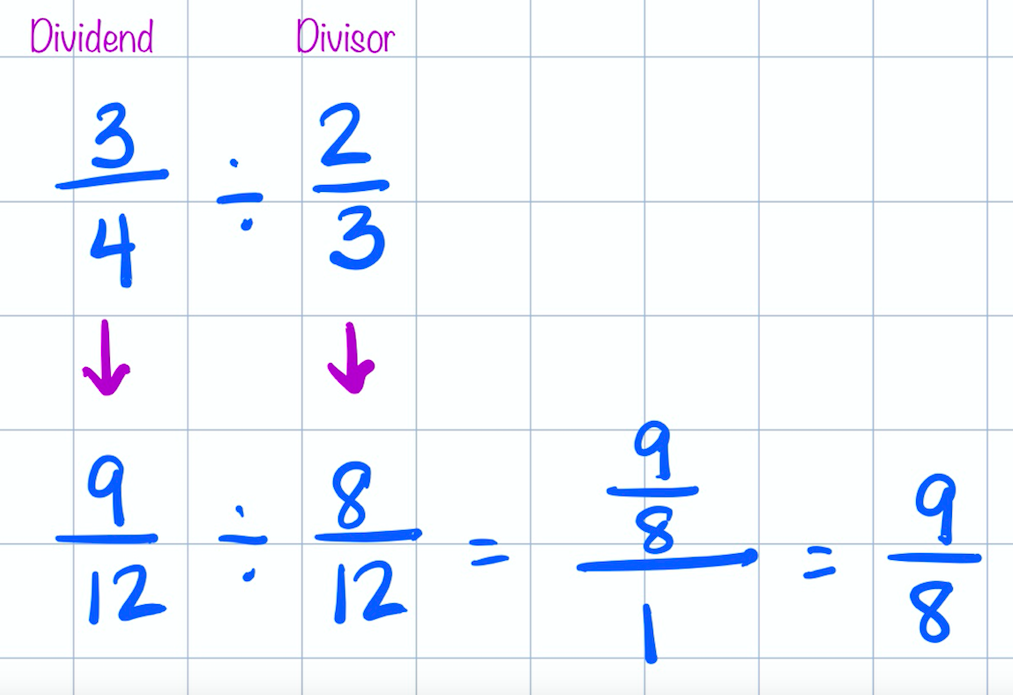
More and more evidence suggests that visualization helps children develop a more conceptual understanding of mathematics. Division involving fractions seems to remain a stumbling block for many. Liping Ma noted in her 1999 work Knowing and Teaching Elementary Mathematics that teachers in the United States had difficulty generating situations that would involve division with fractions - such as sharing the remaining portion of an apple pie or cutting a piece of rope. It was in teaching fraction division that I realized how fragile my own understanding was - and how much I needed to listen to my students and work to connect their thinking. "When we don't ask students to think visually, we miss an incredible opportunity to increase students' understanding and to enable important brain crossing." ~Jo Boaler, Visual Math Improves Math Performance I began with thinking about division with whole numbers. What did we know about division with whole numbers and how might that apply to division involving fractions? Partitive division seemed easiest to model for my students. We began with friendly numbers that we could represent with fraction circles, such as 3/4 divided by 1/3: Students noticed quickly they could overlap the blue pieces on top of the 3/4 to see that 2 blue pieces (each representing 1/3 of a whole circle) would fit. They discovered that the green piece (representing 1/12 of the whole circle) would fill the remaining space. We then needed to figure out how to describe that amount since it no longer represented 1/12 with this model. Students worked to determine that four of the green pieces would equal a blue piece - deciding that the green piece represents 1/4 of the blue piece. We then connected the fraction pieces to symbols, talking about the use of common denominators: As our exploration continued, we wondered whether this method would work with fractions greater than one. In addition to fraction pieces and Cuisenaire rods, we considered tools such as number lines: Using a variety of tools and representations allowed time and space for students to link the meaning of division with the symbolic notation. They had a mental image to manipulate and connect with expressions. And, ultimately, WHY does "keep, change, flip" or "invert and multiply" work? Can we visualize this? This is one way I've thought about it using 3/4 divided by 2/3. I was intentional in using numbers that would be friendly in using an area model but this method would work with any numbers - it just might become too cumbersome to draw! If we multiply both the dividend and divisor by 3/2 (the reciprocal of the divisor), we maintain the relationship between the quantities. We can confirm the quotient of 9/8 using the idea of common denominators described above: I'd love to hear your thoughts about this progression. What are ways it might benefit student thinking? What might potentially interfere with student understanding?
21 Comments
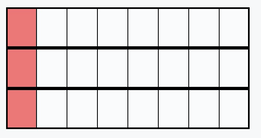
Division with fractions can be perplexing - for adults as well as children. So often, we rely on rules such as "invert and multiply" or "keep, change, flip" that help us perform a procedure but are disconnected to broader mathematical ideas. While done with the best of intentions, creating a model or drawing to help can also interfere with our understanding of division involving fractions. This was evident when tutoring my neighbor this morning. We haven't worked together for a few weeks - last time she was working on addition and subtraction with fractions. Today, we worked on a problem involving making milkshakes. There were 3 cups of chocolate syrup and different recipes: 1/8 cup of chocolate syrup for a chocolate milkshake 2/8 cup of chocolate syrup for a double chocolate milkshake 3/8 cup of chocolate syrup for a triple chocolate milkshake Seems like a simple pattern, right? Once you figure out the number of milkshakes made with one of the recipes, you can use that information to help you figure out the others. My neighbor didn't see the pattern, though. She also wasn't sure why it was a division situation rather than multiplication. When I asked her to draw a picture of her thinking about the problem, she made this: She explained she had seen her teacher draw this in class and it must be 1/8. She was adamant and I realized that the picture caused some interference in her thinking - looking at the picture as a "whole" rather than seeing that there was 1/8 of a cup being used in each row. (If each row represents one cup of chocolate syrup - so the 3 rows would represent the 3 cups of chocolate syrup.) . She was having difficulty distinguishing what was the "whole" - the 3 cups of chocolate syrup versus 1/8 of 1 cup of chocolate syrup. In an effort to help her visualize the repeated removal of 1/8 cup, we tried measuring sugar into bowls. (Unfortunately I didn't have the ingredients for chocolate milkshakes on hand - that would have been more delicious!) After measuring out the sugar, we went back to write equations to match our work. While she seemed a little more confident, she still left our session today still feeling frustrated by fractions. We'll continue to work on multiplication and division with fractions. I'm thinking she might benefit from using common denominators for division to help her see the connection to division with whole numbers. I'm looking forward to our next session to explore these ideas further.
Like many others, I have been choosing one word at the beginning of each year. You can learn more from Jon Gordon's One Word post. I find that the word I choose each year focuses my work. My previous words have been create, empower, and connect. My word for 2019 is believe.
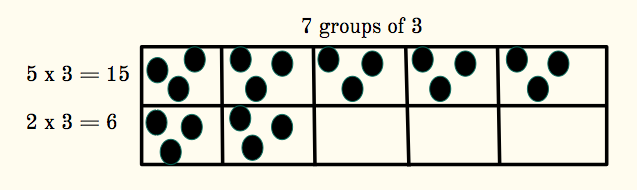
My words have focused my path - from creating a course where students were engaged in rich mathematical thinking to connecting students and teachers with resources and opportunities to expand their definition of mathematics. This year's word is based on my belief that all students can learn when they are provided with access and opportunity. I look forward to continuing to explore how students perceive mathematical ideas. I believe that this is an amazing time to be a mathematics educator. There are so many resources available to share with teachers and students that help us "see" math beyond traditional calculation. Our field is also working diligently to expand the voices that are represented. These connections will only enrich our understanding of mathematics and expand opportunities for our students. Several teachers in my district have been partnering with a professor from the Ohio State University and her graduate students. The conversation among teachers and the influence on classrooms has been incredible. I look forward to continuing to extend this work beyond our current group of amazing educators who bringing inquiry about mathematical ideas to their students. I believe that 2019 is going to be an amazing journey! I can't wait to learn alongside all of you! Just before Thanksgiving, I was working with a 3rd grade teacher and her students to extend the idea of subtilizing and how we might leverage subtilizing to help us visualize multiplication. I used an image of 7 dots from Jo Boaler's work. While the students were not surprised that there were 7 dots, they WERE surprised with the number of ways people saw the dots. Students were eager to share ideas and continued to want to share ideas. After describing 16 different ways to see the dots, we moved the conversation from a whole class conversation to partner conversations. Using playing cards and dice to generate values, students had further conversations about how they "see" the arrangements with their partner. Our next thought is to help students arrange how they might see multiple groupings. For example, how might a ten frame help us organize and see 7 groups of 3? We've collected these ideas from Jo Boaler's Fluency without Fear, Christina Tondevold's Build Math Minds fluency webinars, and Graham Fletcher's work with subtilizing multiplication as well as our own experiences observing students' thinking through the years.
We have a professor from Ohio State working with this class who was also intrigued by the number of ways students "see" the dots. She is wondering about the pattern of how many different ways might be possible. For example, with one dot, there is only one way to see them. With two dots, there are 2 ways (as two individual dots and as a pair). How many ways to see 3 dots? Is there a way for us to predict the number of ways to see a pattern of dots? Would this change if the arrangement of dots changes? Seems like a lot of potential for extensions.... I'd love to hear your thoughts about this activity! Last Thursday, I was fortunate to be installed as the President for the Ohio Council of Teachers of Mathematics (OCTM). In my comments to preservice teachers during our IGNITE session on Friday, I shared that the irony that I hold this office. When I was working on my undergraduate, I was NOT a lover of mathematics. My plans were to become a kindergarten teacher. I loved reading and couldn't wait to share my love of books with my future students! Reading made sense to me. I could spend hours lost in a book - imagining the adventures that were described within the pages. I loved talking about what I had learned and how a book had made me think about other books I had read or events that had happened in my own life. In contrast, my experiences with mathematics had included memorization of rules and procedures - with little opportunity for connections or conversations about the content we were learning. While I performed well, I memorized for the upcoming test and immediately forgot what I had learned. I was hired for my first teaching job as a 4th grade teacher in a small, rural district. During the third or fourth week of my first year, the building principal came to me. She said, "Cindy doesn't want to be the math teacher leader any longer. I'd like you to attend this meeting in October." and handed me a flyer for a math meeting. My first thought was to run the other way - but then common sense prevailed. You don't tell your boss no - especially in the first few weeks on the job! So, I attended the meeting. We were asked to try a sampling lesson about goldfish with our students. (I have found a description of the lesson - keep in mind that this was 1997 and long before standards alignment.) I tried the lesson with my students, expecting them to have no idea how to solve the problem. I had completely underestimated my amazing 4th graders. While they did not get the correct answer, they came closer than I would ever have imagined. Which sparked my curiosity and made me eager to try more experiences like the goldfish lesson. I quickly learned that my students were incredible problem solvers. Listening to students, even to this day, is a powerful reminder that I should never underestimate them! This journey led me to take classes to learn more about how students might engage in mathematics - and ultimately led to the completion of my doctoral degree in mathematics education from the Ohio State University. The credit for this shift in my thinking goes, most importantly, to my students. I have completely relearned mathematics by listening to their ideas. I also credit the support of OCTM in helping me see the structure and beauty of mathematics. This professional organization has meant so much to me over the years. Never was I made to feel like I was an outsider because I didn't like math or because I was an elementary school teacher. Rather, I have always been welcomed and encouraged. The opportunity to give back to this organization that has meant so much to my professional life is a blessing. I am completely humbled by the trust that has been given to me. I am looking forward to helping OCTM continue to grow and serve our mathematics education community in Ohio - and beyond. What can OCTM do for YOU?
When we hear, "Make sense of problems and persevere in solving them" (the first of the eight Standards for Mathematical Practice), we often think of word problems and strategies for comprehension. This standard, however, addresses more than word problems. It is an opportunity for students to seek an entry point and consider ways in which to solve the problem. Students need to self-monitor their progress and try a different strategy if they feel they are not moving towards their goal. While solving problems, students should frequently be asking themselves, "Does this make sense?" Yohaku puzzles are one way you might introduce this thinking into your classroom. I learned about Yohaku puzzles when I attended a meeting of preservice teachers at Baldwin Wallace University a couple of weeks ago. They were doing an activity from NCTM's Teaching Children Mathematics based on a submission from Mike Jacobs to the March 2018 issue. Yohaku means "blank space" in Japanese. Students work to complete the puzzle with numbers that will make the statements true. What a great opportunity for students to practice calculations as they work to confirm whether or not a set of numbers will work! There are often multiple solutions to a puzzle - which can lead to conversations where students prove to one another that their solution is valid. Another topic might be how students know whether or not they have found all possible solutions. I can't wait to try these puzzles with students! If you are looking for an extension to Yohaku puzzles, KenKen puzzles might be a good fit. I used KenKen puzzles with my 5th grade students and they loved them! You can learn more about KenKen puzzles here.
In one question, Sam Shah summarized the frustration I had felt with the accelerated math class I taught for two years. "How does your class move the needle on what your kids think about the doing of math, or what counts as math, or what math feels like, or who can do math?" - Sam Shah in his Call for Presenters for his Virtual Conference on Mathematical Flavors For two years, I had the most wonderful opportunity to teach amazing 5th grade students. Students rode a bus from their home school to spend 75 minutes with me where we delved into rich problems, debated ideas, and created deep connections. Sounds like a dream come true, no? I realized about two weeks into the first year that I was probably not the best person to teach this class. Students had to achieve a particular test score to participate in the class. Mathematics has historically been a "gatekeeper" to opportunity - and I worried about how this class might be sorting students into future "haves" and "have nots". My first year I had 63 amazing mathematicians. My charge was to compact two years of content (5th and 6th grade) into one year so that these students would be ready for the state's 6th grade math test and move into PreAlgebra as 6th graders. It quickly became clear that about 20% of the class could move at a pace that would allow us to meet this goal. I was unwilling to teach "tricks" so I found myself between the proverbial rock and hard place. How to prepare these students while also continuing to build them as mathematicians? I chose to continue focusing on inquiry-based learning and co-constructing mathematical meaning through rich conversations rather than concerning myself with a standardized test. Facilitating these conversations was not always an easy thing to do. Many of my students were brilliant calculators. Speed had taken them far in their mathematics life up to this point. Some were very frustrated when they were asked to explore, invent, and imagine. I was asking them to redefine their view of mathematics. In her book Becoming the Math Teacher You Wish You'd Had, Tracy Zager describes this dilemma: In allowing time for these conversations each day, we eventually built a culture where students made conjectures about mathematical ideas and used reasoning to explain, defend and revise their thinking. By the end of the year, my students used words such as these pictured below to complete the statement "Mathematics is ____." While I felt that I had success in moving the needle for this group of students, I was frustrated by comments made by other teachers. I frequently heard, "Well, of course they can talk about math in those ways. They are the smart kids." I wanted to demonstrate that ALL students can make conjectures about mathematics and reason/debate/revise their thinking about their mathematical ideas. I worried that I was contributing to the idea that mathematics was only for "some" people and I wanted to prove that any student could think deeply about mathematics - not just students who reached a particular score on a test.
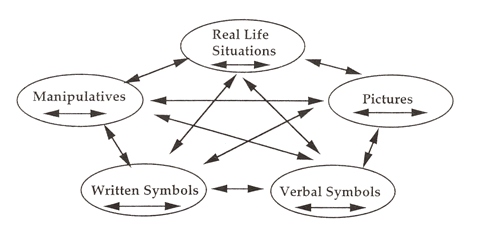
This year, I begin my second year as a math coach in a building where I have the privilege to work with grade K-5 classrooms with diverse learners from different countries and backgrounds. I am blessed to work with an amazing staff who wants to eliminate the traditional idea of mathematics as a gatekeeper. Together, we are working to build mathematical thinkers who are creative and willing to test their ideas. I am grateful for the opportunity to expose each and every student to rich mathematical ideas - without relying on test scores to determine which students will access these experiences. I can't wait to see what students notice and wonder this year about mathematics! I know I will learn a lot from them and I am looking forward to a wonderful year! "If you could have secondary teachers understand one thing about elementary school math learning, what would that be?" - David Sabol (@Dave_Sabol) As an elementary school teacher and instructional coach, I am so appreciative of this question. And especially that so many teachers from #TMC18 are asking about what we do in elementary school mathematics. I think these conversations are essential in helping us all learn together and provide a more cohesive experience for all of our students. Using and connecting representations is a huge part of our work in elementary school - along with providing many opportunities for conversation to make sense of mathematical ideas. In conversations with teachers, I often refer to the image below from Lesh and his colleagues to show how these representations are connected in making sense of mathematical ideas. Through these multiple representations, students deepen their understanding of the mathematical content. In Ohio, our standards are written so that students move from concrete to iconic/pictorial to abstract/symbolic representations. Some of these ideas build across years - which gives learners the time and space to develop these ideas in a deeper and more connected way. They have the opportunity to build, then draw, and then use symbolic notation to represent their mathematical ideas. Throughout this process, there would be many conversations and writing about their ideas as they connect these different representations. (Let me be clear - this is something we are still working on and I am not claiming that we have it all figured out at the elementary school level! We are improving at making these connections and deepening our conversations about mathematical content.) In the photos below, you can see 1st grade students using blocks, pictures, equations, and apps such as Number Line to represent their ideas about Graham Fletcher's Bright Idea 3-Act Task. Students worked in groups to refine their ideas and then shared during a whole class conversation. In the next example below, 3rd grade students worked in groups to write a story about creating bouquets of flowers. The groups were then asked to draw a picture and write an equation that would match the story. During the class conversation, students were looking to see whether the story, equation, and picture were a match. This video provided a chance to see students working to make sense of what these different representations mean and how they might be connected to the mathematics and context of the problem. In the following example, 5th grade students debate whether the answer to a problem is 4/5 or 4/7. I was fascinated by how what students knew about addition and multiplication of fractions interfered with their ability to make sense of this problem: In a bag, 3/5 of the marbles are blue and the rest are red. If the number of red marbles is doubled and the number of blue marbles stays the same, what fraction of the marbles will be red? I thought this would be a quick warm-up exercise - instead it turned into a debate that lasted 30 minutes and continued to the next day. (Which made for fantastic discussion!) I see these classroom conversations as essential to empowering students to think mathematically. Robert Berry describes this eloquently in his post Positioning Students as Mathematically Competent. What types of conversations are happening in secondary mathematics classrooms? How does what we do in elementary school influence what comes later? What can we do as elementary school teachers to build stronger coherence for our students? I would love for there to be further conversation between elementary and secondary mathematics teachers. We have so much to learn from one another!
I've been using Jon Gordon's One Word to set a goal for myself each year. This year's word is CONNECT. Spending 4 days at Twitter Math Camp (TMC) this past week allowed me so many ways to live my word! The event was in Cleveland, OH and I was fortunate to be going with two amazing colleagues from my district (@brendaboring1 and @kellykir02). Sharing this experience allowed us to connect at both a professional and personal level and I'm looking forward to how we might share what we have learned throughout our district.
It was incredibly powerful to spend time with like-minded educators who are working to provide the best possible opportunities to help students learn mathematics. We had conversations around equity, engagement, content, pedagogy - along with some time for fun! I'm still processing all of the information we discussed but I know our conversations will deeply impact my work this year. Some ideas I want to remember are the powerful message shared by @DingleTeach about measures of center and how we can make ALL feel welcome and valued. I also want to remember the importance of being a teacher leader (thank you for the inspiring message that we ARE enough, @jreulbach) - which is important in working to push forward actions of inclusion and equity. I loved meeting new people close to home (@MrKisselMATH, @minor_math, @sail2pib and @MrsArnoldPlus1) as well as from across the country and beyond (@MsSpinato, @bstockus, @madisonsandig4, @robertqberry, @saravdwerf, @gfletchy, @jryske, @beske3, @davidpetro314, @MFAnnie, @joshchanyh, @Kidsmathtalk and so many others). Having the opportunity to talk in person will enrich the connections and conversations we have on Twitter. A heartfelt thank you to @lmhenry9, @Dave_Sabol, @crstn85 and all of the organizers of #TMC18. I know it is a tremendous amount of work to organize a conference and I am so appreciative to have had the opportunity to participate in this transformative experience! Thank you to @batty314 for sharing about #TMC17 - you were right about TMC being the best PD ever! If you are looking to engage with educators passionate about the learning of mathematics, I strongly encourage you to follow the people I've mentioned. They are just a few of the amazing people who make up the #MTBoS community. I'm looking forward to continuing to connect with this community! Thank you for your energy and commitment to mathematics education! Too often, we miss opportunities to connect with the families of our students. Parents want to be involved in their children's education and our students will benefit when parents and teachers work in partnership. Math might be intimidating for some - especially when the focus is on justifying ideas or asking questions - since this way of thinking is very different from how many people experienced school mathematics. Our school has held family math nights and our classroom teachers communicate regularly with families. We are continually looking for ways to improve this partnership. This past school year, our staff watched Dan Finkel's TedTalk "Five Principles of Extraordinary Math Teaching". It is one of my favorite messages for teachers and parents alike. The message emphasizes the importance of play in mathematics and provides practical advice. As educators, we have spent time working with parents about having books available and reading with children at home. Many parents feel comfortable reading with their child and talking about books. We have not, however, always provided specific ideas and support for parents in regards to mathematics. In our grade level teams, we brainstormed ways families could interact with math at home. Our ideas included picture books, real-world applications, and games. A website seemed an efficient way to share the information with families that would allow us to update information and expand on our ideas over time. We included a weekly challenge so that the website changes each week - there is new information for families and a reason to return. Click on the image below to see our work. I would love to hear your thoughts about our website and ways that you partner with parents!
|
AuthorSharing what I'm learning from others. Collaborative experiences and communication are essential in building a shared understanding of mathematics! Archives
September 2018
Categories |



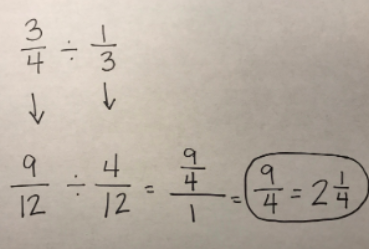













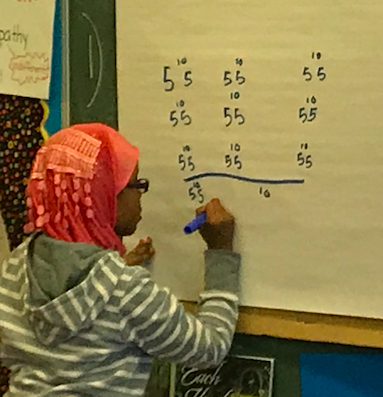

 RSS Feed
RSS Feed
